引言
Gestalt Laws(格式塔法则)
- Law of Proximity:人们自然而然的对靠近的事物进行分组
- Law of Similarity:人们在观察对象时容易把相思的物体分成一组
- Law of Common Fate:对象容易被视为行进在光滑路径上的线条
- Law of Symmetry:人们观察对象时容易将对象视为对称的且围绕一个中心
- Law of Continuity:对象的元素容易群聚在一起,且能形成整体
- Law of Closure:人们在观察诸如形状、信封、照片时自动补全他们
Marr视觉表示框架的三个阶段
- Primal Sketch:将原始图进行处理,抽取角点、纹理等基本特征,这些特征的集合称为基元图
- 2.5D Sketch:以观测者为中心的坐标系中,由输入图像和基元图恢复场景可见部分的深度、法线方向、轮廓等等,这些信息包含了深度信息,但不是真正的物体三维表示
- 3D Model:以物体为中心的坐标系中,由输入图像、基元图、2.5D图来恢复、表示和识别三位物体
二值图像
几何特性
- 面积(零阶矩)
- A = ΣΣ B[i,j]
- 区域中心(一阶矩)
- x = ( ΣΣ jB[i,j] )/ A
- y = ( -ΣΣ iB[i,j] )/ A
- 方向
- 某些形状是没有方向的
(比如你南球) - 假定物体是长方形的,长轴方向为物体的方向
(比如KKE的腿) - 求方向:转化为最小化问题
- χ^2 = ΣΣr_ij^2 B[i,j] r_ij是点(i,j)到直线的距离
- 求解方式:最小二乘
- 某些形状是没有方向的
- 伸长率
- E = χmax / χmin
- 密集度
- C = A/p^2
- p是周长,A是面积
- 给定周长,密集度越高,围成的面积就越大:圆 > 正方形 > 长方形
- 形态比
- 区域的最小外接矩形的长宽比
- 欧拉数(亏格数,genus)
- 连通分量数 减去 洞数
- E = C - H
- 平稳、旋转和比例不变
- 字母A:E=1-1=0,字幕B:E=1-2=-1,字母C:E=1-0=1
投影计算
- 定义:给定一条直线,用垂直该直线的一簇等间距直线将一副二值图像分割成若干条,每一条内像素值为1的像素的数量。
- 水平投影、垂直投影:可以看做将图像给一个重力,全部降落到x轴/y轴并堆叠起来
联通区域
- 四连通:上下左右(和自己)联通;八连通:左上、右上、左下、右下也算连通
- 连通定义:已知像素p,q∈S,如果存在一条从p到q的路径,且路径上全部像素都包含在S中,则称p与q是连通的
- 连通关系是等价关系,具有自反性、互换性和传递性
- 连通分量的定义:连通像素的集合
联通分量标记算法
递归算法
- 扫描图像,找到没有标记的一个前景点(即像素值为1/黑的/和背景的白块相对),分配标记L
- 递归分配标记L给该点的邻点
- 如果不存在没有标记的点,则停止
- 返回第1步
序贯算法(4连通)
- 从左到右、从上到下扫描图像
- 如果像素点值为1,则分4种情况:
- 如果上面点和左面点有且仅有一个标记,则复制这一标记
- 如果两点有相同标记,复制这一标记
- 如果两点有不同标记,则复制上点标记,且将两个标记输入 等价表 中作为等价标记
- 否则给这一个像素点分配一新的标记,并将这一标记输入等价表
- 如果需要考虑等多点,则返回2
- 在等价表的每一等价集中找到最低的标记
- 扫描图像,用等价表中的最低标记取代每一标记
区域边界跟踪算法
c:当前点(在边界上) b:当前点的领域点(不在边界上)
- 从左到右,从上到下扫描图像,求区域S的起始点
- s(k) = ( x(k), y(k) ), k = 0
- 用c表示当前边界上被跟踪的像素点,置c = s(k),记c的左邻点为b,b∈S^-
- 按逆时针方向记从b开始的c的8个8邻点分别为 n1, n2, … , n8,k = k+1
- 从b开始,沿逆时针方向找到第一个ni∈S
- 置c = s(k) = ni, b = ni-1
- 重复步骤3,4,5,直到s(k)=s(0)
边缘
模板卷积
T*I(X,Y) = ΣΣ T(i,j) I(X+i,Y+j)反正矩阵里每一个元素用模板算一下就行了
Origin of Edges
四种最主要的不连续(discontinuity)
- surface normal discontinuity
- depth discontinuity
- surface color discontinuity
- illumination discontinuity
边缘检测的基本思想
- 函数导数反映图像灰度变化的显著程度
- 一阶导数的局部极大值,或二阶导数的过零点
基于一阶的边缘检测
- 梯度
- 幅值:| G(x,y) | = sqrt( Gx^2 + Gy^2 )
- 方向:a(x,y) = arctan( Gy/Gx )
- 梯度方向是函数最大变化率方向
- 图像中用差分近似偏导数
- Roberts交叉算子
- Sobel算子
- Prewitt算子:运算较快
基于二阶的边缘检测
Laplacian(拉普拉斯)算子
- 二阶导数的二维等效式
- 表示为卷积模板 ▽^2 =
0 1 0
1 -4 1
0 1 0 - 领域中心点具有更大权值的近似算子:
1 4 1
4 -20 4
1 4 1
LoG算子(Marr&Hildreth算子)
LoG = Laplacian of Gaussian 高斯滤波+拉普拉斯边缘检测
基本特征
- 平滑滤波器是高斯滤波器
- 采用拉普拉斯算子计算二阶导数
- 边缘检测判据是二阶导数零交叉点并对应一阶导数的较大峰值
- 使用线性内插方法在子像素分辨率水平上估计边缘的位置
两种等效算法
- 图像与高斯函数卷积,再求卷积的拉普拉斯微分
- 求高斯函数的拉普拉斯微分,再与图像卷积
使用高斯滤波器的原因
平滑去噪和边缘检测是一对矛盾,应用高斯函数的一阶导数,在二者之间获得最佳的平衡
Canny边缘检测
算法步骤
- 用高斯滤波器平滑图像
- 用一阶偏导有限差计算梯度幅值和方向
- 对梯度幅值进行非极大值抑制(NMS)
- 将梯度角离散为圆周的四个扇区之一,以便用3*3的窗口作抑制运算
- 方向角离散化(离散到每一个Sector上)
- 抑制,得到新幅值图:如果M[i,j]不比梯度线方向上的两个相邻点幅值大,则N[i,j]=0
- 用双阈值算法检测和连接边缘
- 取高低两个阈值(T2, T1)作用于新幅值图N[i,j],得到两个边缘图:高阈值和低阈值边缘图
- 高阈值图:N[i,j] > T2
- 低阈值图:N[i,j] > T1
- 连接高阈值边缘图,出现断点时,在低阈值边缘图中的8邻点域搜寻边缘点
- 阈值太低:假边缘
- 阈值太高:部分轮廓丢失
- 因此选用两个阈值是更有效的阈值方案
- 取高低两个阈值(T2, T1)作用于新幅值图N[i,j],得到两个边缘图:高阈值和低阈值边缘图
局部特征 Local Feature
Harris角点检测
- 原理:一个窗口在图像上移动。平滑区域里,在各个方向上都没有变化;边缘上,在边缘方向没有变化;角点,在各个方向都有变化
- 窗口平移[u,v]产生的变化E(u,v) ≌ [u,v] M [u,v]^T
- If u,v are small values, I(x+u, y+v) = I(x,y) + uIx(x,y) + vIy(x,y)
- E(u,v) = Σw(x,y)[I(x+u,y+v) - I(u,v)]^2
- = Σw(x,y)( uIx(x,y) + vIy(x,y) )^2
- = [u,v] ( Σw(x,y)[ Ix^2 IxIy \ IxIy Iy^2 ] ) [u,v]T
- ≌ [u,v] M [u,v]^T
- I(x,y)是强度 Ix和Iy是M特征根
- R = del M - k(trace M)^2
- del M = λ1λ2
- trace M = λ1 + λ2
- 另一种表示:R = λ1λ2 - k(λ1+λ2)^2
- |R| small: Flat
- R > 0: Corner
- R < 0: Edge
SIFT描述子的计算
MR和IA已经看了两次了
- 计算的基本步骤
- 为什么只使用梯度信息
- 如何实现旋转不变
- 因为旋转的时候每一个关键点周围的店也会跟着旋转,不会影响SIFT向量。所以SIFT对旋转不敏感
尺度不变的原理
- 因为金字塔模型,对每一种尺度都能进行检测,所以具有尺度不变性
曲线
曲线表示
曲线表示
- 显示表达:Explicit
- y = f1(x)
- y = f2(x) ???
- 隐式表达:Implicit
- f1(x,y) = 0
- f2(x,y) = 0
- 参数表达
- r, θ
曲线离散化
- 曲线长度
s = Σ sqrt( (xi - xi-1)^2 + (yi - yi-1)^2 ) - 曲线切向量(k斜率)
φ = arctan( (yi+k - yi)/(xi+k - xi) ) - 曲率(k曲率)
Θ = φl - φr
曲线拟合
概念:给定一系列边缘点,设法找到一条曲线的函数表达式,通过调整参数尽量使该曲线接近所有的边缘点以描述对象的轮廓
Douglas-Peucker算法
对每一条离散曲线的首末点虚连一条直线,求所有点与直线的距离,并找出最大值dmax,用dmax于阈值D相比:
- 若dmax < D,这条曲线上的中间点全部社区;
- 若dmax >= D,保留dmax对应的点,并以该点为界,把曲线分为两部分,对这两部分重复使用该方法。
Hough变换直线检测
Hough变换是基于投票原理的参数估计方法
- 基本思想:图像中每一点对参数组合进行表决,赢得多数票的参数组合为胜者(结果)
直线检测
y=mx+c -> c=-xm+y
以(x,y)为自变量,(m,c)为因变量,每个点(x,y)对应于空间(m,c)上的一条线
为了避免垂直直线所带来的问题,采用极坐标表示:
ρ = xcosθ + ysinθ
同一条直线的ρ和θ是相同的,因此所有属于同一条直线上的点会在参数空间交于一点
- 适当的 量化 参数空间
- 假定参数空间的每一个单元都是一个累加器,把累加器 初始化 为零
- 对图像空间的每一点,在其所满足的参数方程对应的累加器上 加1
- 累加器阵列的最大值对应模型的参数
图像频域
图像的傅里叶变换
AΣ(1/k)sin(2πkt)
- 基本含义:一个函数表达成三角函数或者他们的积分的线性组合
- 图像的低频成分与高频成分:你懂的
怎么理解拉普拉斯金字塔的每一层是带通滤波
因为是高通减低通
人脸识别
主元分析(PCA)
- PCA方法作用以及意义
- 优化目标函数的推导
d维空间x=(x1, … ,xd),投影方向a1=(a11,a12, … ,a1d)^T,a1a1^T = 1
投影值z1=a1^Tx=Σa1ixi
问题:最大化var(z1),求投影方向argmax_a1 var(z1)
因为 var(z1) = a1T S a1
其中 S = E(xi,yi) - E(xi)E(yi) = Cov(xi, yi)
所以就是最大化 a1T S a1,其中a1T a1 = 1
解:
设λ为Lagrange乘子,转为最大化 a1T S a1 - λ(a1T S a1)
以a1T为变量,对上式求微分,令微分为零。
S a1 - λa1 = 0
S a1 = λa1
观察上述表达式,就是矩阵特征值的定义
所以必须用协方差矩阵最大特征值对应的特征向量,转化为求协方差矩阵
Eigenface
- Eigenface的含义
- Eigenface人脸识别方法的基本步骤
- 重构的含义,以及用于人脸检测的原理
相机模型(一)
理解:景深/光圈/焦距/视场
- 光圈对景深的影响?能用图示解释
大光圈景深小,小光圈景深大
光路图里把上下两条线放近一点 - 焦距对视场的影响?能画图用公式表示
φ = tan^-1( d/2f ) φ是视角的二分之一
大焦距 离得近 (整个场景被缩短|远处的东西被拉到近处而且很大|但是虚化了|焦距内的物体也能看到
小焦距 离得远 (整个场景被拉长|远处的东西很小|但是都很清楚|焦距内的东西会在视野外
总之就是焦距越大,视场越小
理想的针孔相机(pinhole camera)模型
基本投影公式,并能画图说明,回写其次坐标形式下的透视投影公式(矩阵形式)
x/f = X/Z
有哪几个内参(不包括畸变参数)?回写内参矩阵
(fx, fy, cx, cy)
fx = F sx, fy = F sy
cx,cy:主点
q = MQ, 像素值 q = [x,y,w]^T, M = [fx, 0, cx\0, fy, cy\0, 0, 1], 物理尺寸 Q = [X, Y, Z]^T
相机模型(二)
畸变
- 径向畸变
- 原因是光线在远离透镜中心的地方比靠近中心的地方更加弯曲
- 桶形畸变:中间向外凸起
- 枕形畸变:中间向内凹陷
- 切向畸变
- 原因是透镜不完全平行于图像平面
外参有哪几个?分别代表什么含义?
(θ, φ, ψ, tx, ty, tz)
似乎转换成了(fsx, xc, fsy, yc)
内参、外参、畸变参数在成像各阶段中的角色(从三维物体到真实图像的过程)
畸变参数:(k1, k2, p1, p2, k3)
k和径向畸变有关,p和切向畸变有关
相机定标
相机定标需要求解哪些参数
基于棋盘/Homography的相机定标
- 基于棋盘的相机定标:已知什么?求解什么?
- 件数其基本过程哪几个步骤?
立体视觉
立体视觉的三角测量基本原理(Triangulation公式)
- 会画算“视差disparity”的那张图,并能推导公式
Triangulation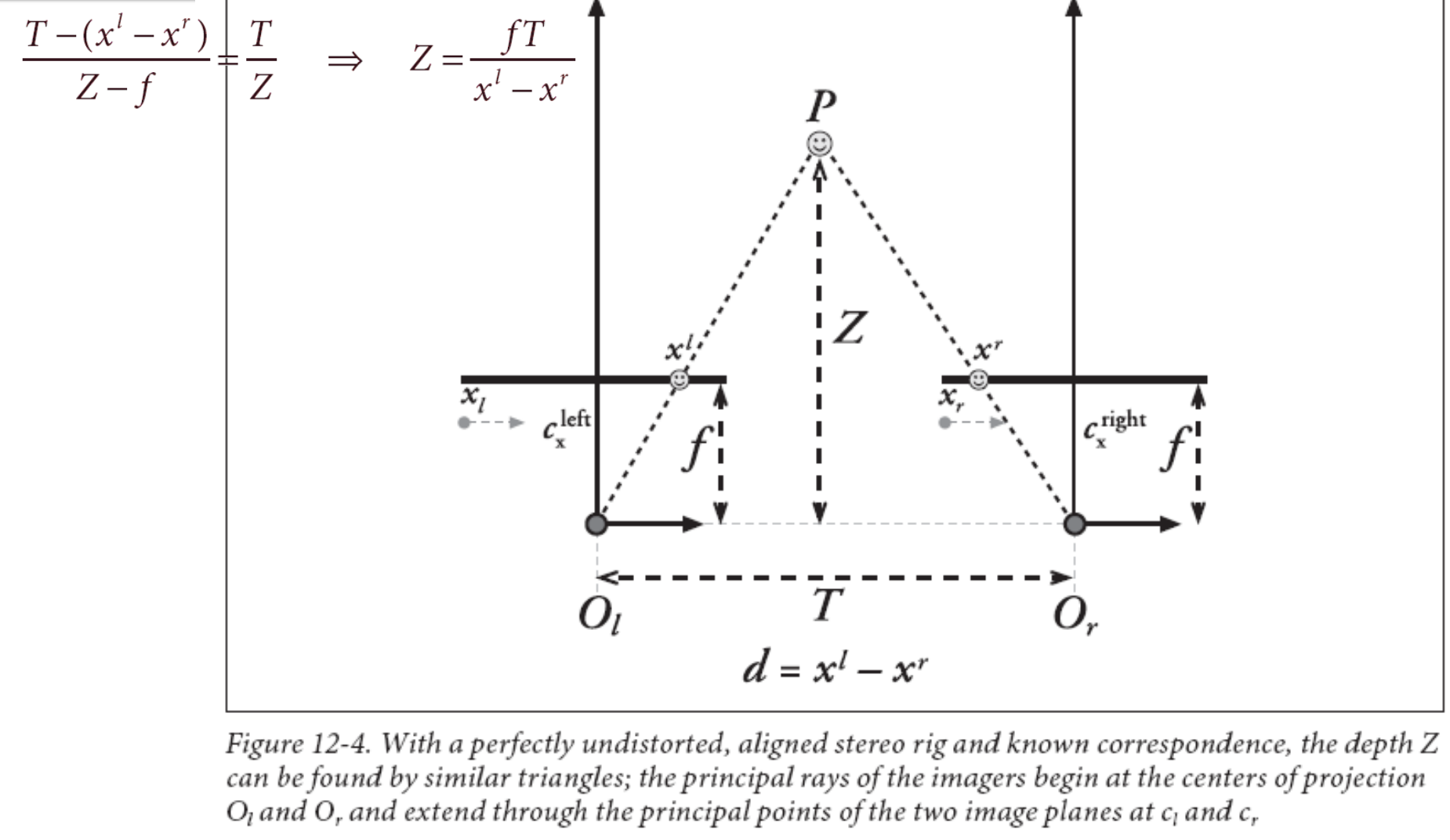
使用三角形相似
Z = fT / (xl - xr)
立体视觉的基本步骤(Review: How to Do Stereo)
- 消除畸变
- 校正相机(Rectification)
- 两幅图中找到相同特征
- 三角测量
为什么要做校正(Rectification)
呀
Stereo matching的基本步骤(校正之后)
for each epipolar line
for each pixel in the left image
compare with every pixel on match cost
pick pixel with minimum match cost
But this will never work, so improvement: match WINDOWS
三维数据获取
结构光成像系统的构成
利用结构光获取三维数据的基本原理
- 会画图,会推导公式
Structured Lighting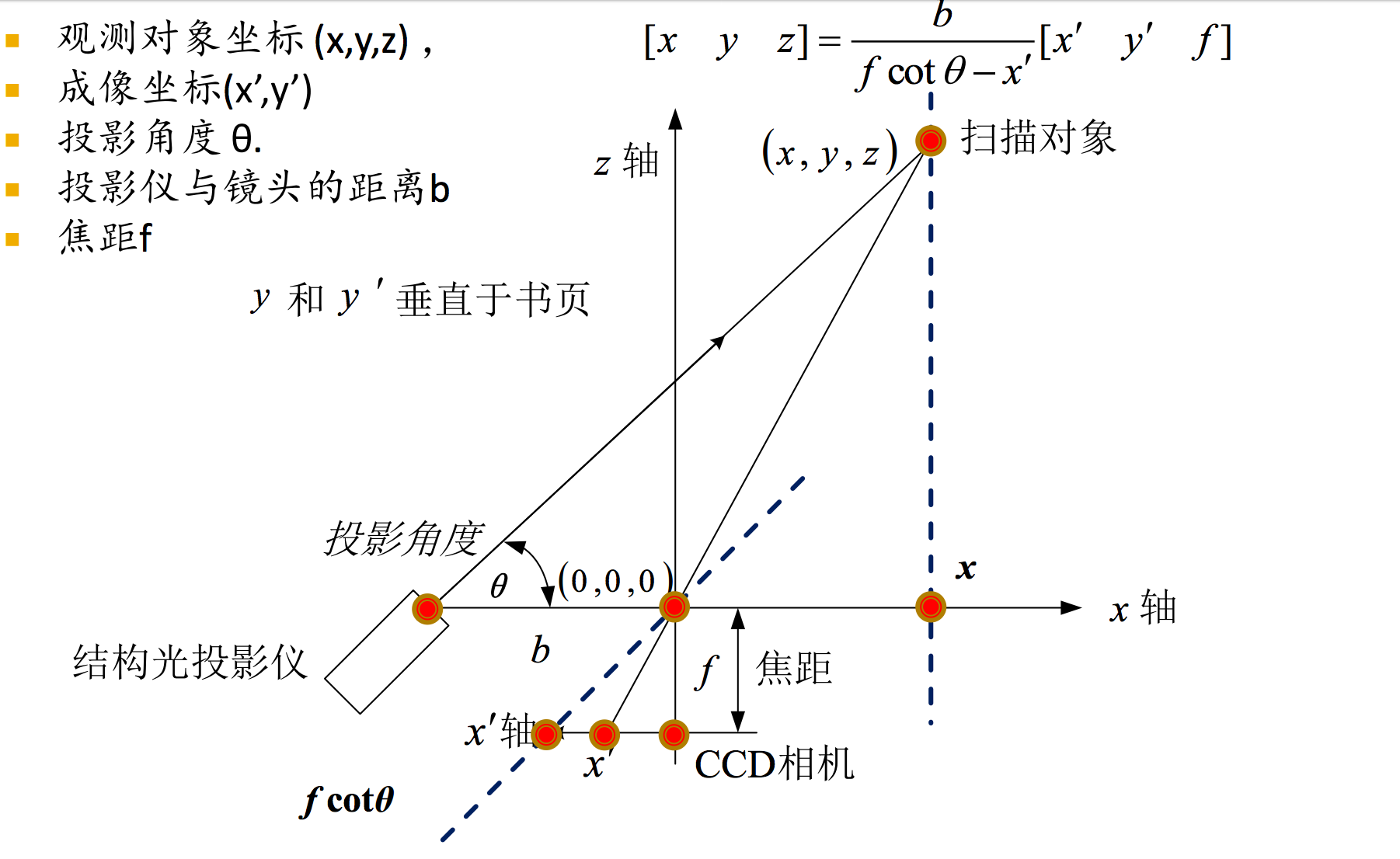
光流
光流解决的是什么问题
pixel correspondence problem:像素对应问题
H、I两幅图,给定H中的一个坐标,在I中的附近坐标找到同样的
光流三个基本假设是什么
- brightness constancy 亮度恒定
- spatial coherence 空间相干性
- small motion 小移动
一个点的约束公式会推导
O = It + ▽I·[u v]
u,v都是小量
推导:
O = I(x+u, y+v) - H(x,y)
≈ I(x,y) + Ixu + Iyv - H(x,y)
≈( I(x,y) - H(x,y) ) + Ixu + Iyv
≈ It + Ixu + Iyv
≈ It + ▽I·[u v]
哪些位置光流比较可靠?为什么?
图像分割
图像分割的目标是什么
Group Pixels into meaningful or perceptually similar regions
像素集合转换成有意义的或感觉上相似的区域
基于k-means聚类的图像分割
- 理解用聚类进行图像分割的基本原理
- 给定一副图像,能描述如何用k-means进行分割的算法基本步骤(除了k-means算法本身的几个步骤之外,还自己总结添加k-means之前做什么、k-means之后做什么)
IA看过了 - 之前要提取SIFT特征
- 之后要构建
物体识别
Visual Recognition有哪些目标
- Classify images or videos 图像和视频分类
- Detect and localize objects 检测和定位对象
- Estimate semantic and geometrical attributes 估计语义和几何属性
- Classify human activities and events 分类人类活动和行为
基于词袋(BoW)的物体分类
图像的BoW(bag-of-words)是指什么意思
基本步骤
- Feature extraction and representation 特征提取和表示
- Building codebook (codewords dictionary) from training samples with clustering 从训练样本中建立码本
- Represent an image with histogram of codebook (i.e. Bag-of-words of an image) 将码本的直方图表示为图像
- Classify an unknown image with its BoW. 用这个BoW对未知图像做分类